O čem to je?

Bitcoin

Tento odstavec tu původně nebyl, ale nakonec se přece jenom pokusím i o stručné shrnutí, co to je Bitcoin, protože díky (kvůli) němu vlastně tyto stránky vznikly.

Bitcoin jsou peníze.

Bitcoin jsou globální nestátní neutrální peníze.
Globální - mohou fungovat po celé Zemi, časem klidně i na Měsíci nebo na Marsu.
Nestátní - původně jsem více uváděl decentralizované - nemají žádného "šéfa", ale státy a jejich vlády nám do peněz zasahují nejvíce, proto je toto hlavním přínosem decentralizace.
Neutrální - je jim jedno, kdo je má - bohatý chudý / černý bílý / podvodník svatoušek.... 

Jedna z jeho základních částí je open-source program, o kterém si každý může ověřit (nebo tím někoho pověřit), jak funguje. A v principu je jednoduchý.
Bitcoin je blbuvzdorný a vzácný. Je tak navržen. Počítá s tím, že se ho někdo bude snažit rozbít nebo zneužít.

Rozlišuje se bitcoin ("peněžní" jednotka) a Bitcoin (technologie).

Vlastnit nějaký druh kryptoměny (například „vlastnit bitcoin“), znamená znát tajné heslo (privátní klíč) k nějaké peněžence (veřejný klíč) a tím mít dispoziční právo k nakládání s „obnosem“ v dané peněžence.
Bitcoiny nejsou ani v mobilu, ani v Trezoru – elektronická zařízení slouží jen jako rozhraní, které autorizuje naše požadavky na změny v Blockchainu.

K uchování privátního klíče pomůže „seed“ (semínko)

 Aby byl privátní klíč dostatečně bezpečný musí být poněkud delší:

a865acb485c2b8782a2f63a888ceb6d3226dd28b2c10ea314b71d455680f5609fe04afc833681078054126a03c77ac99f1396e1426fd438034be9b8dababde3f

Privátní klíč má délku 256 bitů:
Kdyby měl délku jeden bit, mohl by nabývat dvou možných hodnot – nula nebo jedna – a „generoval by se jediným hodem mincí. Padla by panna nebo orel. Hod mincí dvakrát za sebou už může být ze čtyř možných kombinací:
0,0 – 0,1 – 1,0 – 1,1
no a při házení mincí třikrát za sebou, už je to kombinací osm:
000, 001, 010, 011, 100, 101, 110, 111
2¹ = 2
2² = 4
2³ = 8

Možná znáte historku, podle které si výherce hry šachy vyžádal „prostou odměnu pár zrnek obilí“, kdy na první políčko bylo položeno jedno zrnko, na druhé dvě, na další čtyři (dvojnásobek) pak 8, 16, 32, 64, 128, 256, 512, 1024 … na což vládce přistoupil, ale už v polovině šachovnice byla královská sýpka prázdná… (políček je 64 = 8×8, a polovina je 32)
2³² = 4 294 967 296 (plná hrst zrní je například 10 000 zrnek, a pytel může být 1000 hrstí? takže nám zde vychází už 429 pytlů plných zrní!) | Část o velkých číslech byla přesunuta na samostatnou stránku.
2⁶⁴ = 18 446 744 073 709 552 000

Takže při délce 256 bitů se generuje z množiny 2²⁵⁶ čísel. To znamená, že v binárním tvaru jde o řetězec z nul a jedniček dlouhý 256 znaků (0/1).
Ono to je o něco méně, pár znaků se vyhradilo na další hierarchické členění (protože to úplně postačí) takže nepatrně zkrácený privátní klíč je například toto:

11000111010010100110111100110100011110001110010111110011000111101001111011111101001101001100111110001111000111000010101101010010111101111100110011101011101001001010111011110010001011000111001011010110001011001011110011100000111010001110010101100011110011101111010001101000110001101100101101001011011011110010111001110000110001111010000110001110010111101000

wallet_privkey (bin-> base58):  cRM9QqeyGSo44gccBZKoLu4JwHXr5EK3AhrXy7QQFeRmr9aGPcK
(h)

Jak to bezchybně opsat pro potřebu zálohy? První uživatelé Bitcoinu se s tím trápili a hledali nějaké zjednodušení. A proto vznikl mnemonic seed (dle BIP39):
Privátní klíč (delší řetězec znaků a čísel) se pohodlněji a spolehlivěji uchovává pomocí seedu – což je nejčastěji 12 anglických slov. Varianta je i 24 či jiný počet a existuje i v dalších jazycích) ze kterých aplikace (mobilní nebo počítačové peněženky) umí privátní klíč sestavit (generovat a následně i derivuje všechny potřebné adresy – peněženky).

Což může vypadat takto:
(záměrně jsme vybrali seed z jiného zdroje)

army van defense carry jealous true 
garbage claim echo media make crunch

Tento seed patří mezi nejznámější ukázky a tudíž je maximálně „zdiskreditovaný“ (protože byl veřejně publikovaný je pro ostatní uživatele prakticky nepoužitelný, nemá žádný „kredit“, veškeré prostředky tam poslané si může kdokoli „vzít“ (přeposlat k sobě), ale využívá se jako příklad – například v knize Mastering Bitcoin (autor: Andreas Antonopoulos) nebo na detailnějších ukázkách „zdrojových dat“:
https://bitcoin.stackexchange.com/questions/84116/get-master-private-key-from-bip39-seed

Jak se z jedniček a nul stane lépe člověkem čitelná a „přepsatelná“ varianta?
Vrátíme se k původní ukázce jedniček a nul, kterou použijeme k vytvoření vlastního seedu. Zde již není zdiskreditovaný celý seed, ale kdo si vezme zdrojová data, může si ho sestavit celý (což už ale vyžaduje hlubší znalosti).

Takto vypadá převod „binárních čísel na slova“.

Uchování privátního klíče však na dva základní protichůdné požadavky:
1. Musíme ho mít uložen bezpečně tak, aby nás o něj někdo nemohl připravit.
2. Musíme ho ale mít možnost „obnovit“ – a tedy mít i pláb B, abychom ho definitivně neztratili.

Některé nástroje [python] pro práci s PK a podobně:
https://github.com/octopusengine/crypto_agama

Je privátní klíč opravdu tak bezpečný?

Privátní klíč má délku 256 bitů, takže se generuje z množiny  2²⁵⁶  čísel.
 2²⁵⁶ =    115,792,089,237,316,195,423,570,985,008,687,907,853,269,984,665,640,564,039,457,584,007,913,129,639,936
=  10⁷⁷  (deset a sedmdesát sedm nul - zaokrouhleno)
Tolik privátních klíčů se dá náhodně podle daného popisu vygenerovat. 
Kolik to asi je? Můžeme si to nějak "představit"?

Na Internetu je to všechno dostupné: https://lbc.cryptoguru.org/dio/
(pointou je, že to je generovaná hříčka – a ne databáze, která by vám vyhledala zpětně PK 😀 ale dost lidí kvůli tomu Bitcoinu trochu nedůvěřuje).

Mám takovou analogii: představte si zrníčko jemného písku, kterých je v krychlovém milimetru zhruba tisíc(10x10x10 – aby se to dobře počítalo).
V kouli o průměru 62 cm (1 m³) to je už zhruba 10⁹⁺³= 10¹² zrníček, což je zatím „vyslovitelných“ tisíc miliard (bilión česky, trilion anglicky). To je přibližně šestnáct stavebních koleček plných písku. Představte si, že vám je přiděleno jediné zrnko – jako váš privátní klíč. Kdyby mělo odlišnou barvu, asi ho po nějaké době v jednom kolečku najdete. Dá to asi práci, ale najdete. Ale jdeme dál, ono jich je víc. Víc než v nějakém lomu? Nebo na nějaké mořské pláži? Víc než na všech plážích světa?

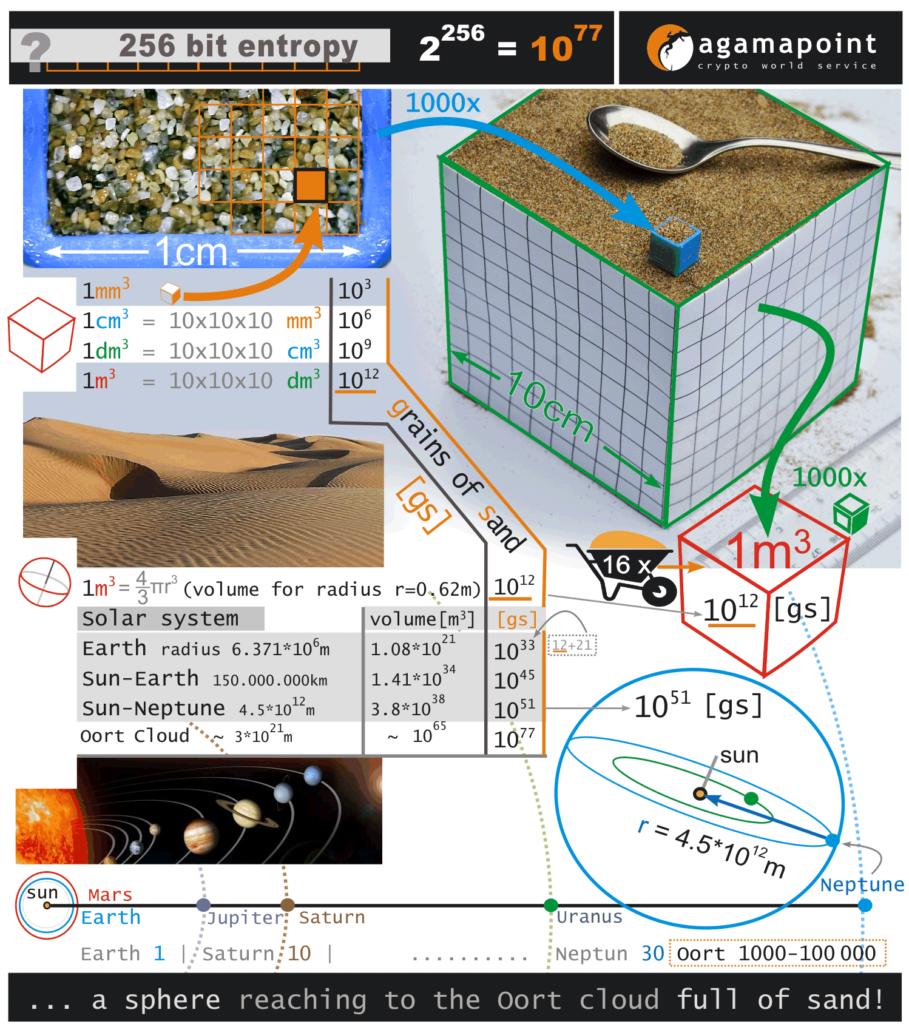
Těch zrníček je 10⁷⁷ – což zabírá objem 10⁶⁹ m³.
No a to je koule o průměru …. třetí odmocnina z 2.28 * 10⁶⁸ je…. něco * 10²² m,
což je koule o průměru 10¹⁹ km, plná písku. Uf.
Planeta Neptun je od Slunce vzdálená 4 * 10⁹ km. Musíme vzít v úvahu kouli zahrnující Oortův oblak Sluneční soustavy – plnou písku.

Objem Země je cca 10¹² km³ což je (…12 [km] +3*3 [m] +8 [gs] = 29) 10²⁹ zrnek písku.
Pro 10⁷⁷ by bylo potřeba (77-29) 10⁴⁸planet velikosti Země!

Představte si tedy všechny planety viditelného vesmíru s pískem na povrchu. Tak toho písku je zhruba tak (respektive pořád o něco víc, ta planety by všechny mohly být celé z písku! I jejich Slunce. Všechno z písku!)

A tam hledejte své jedno zrnko!

 All Bitcoin private keys is simply an integer between number 1 and 115792089237316195423570985008687907852837564279074904382605163141518161494337 or HEX: from 1 to 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141.