Chaos (deterministický)

Nemá cenu si dělat svět složitější, než je, o to se rozhodně tímto článkem nesnažím – naopak, rád bych „zjednodušil“. Ale mysleme na to, že těch opravdu jednoduchých věcí v přírodě moc není. Přírodní systémy jsou většinou nelineární, těsně vzájemně svázané – a v tom právě spočívá jejich rozmanitost a krása.

Motto: Jestliže je věda čtením a luštěním přírody, primární zkoumání se musí týkat znamení, jichž příroda užívá, aby skryla či zjevila svůj půvab.

https://chaos.hcpp.cz/
Hackers Congress PP 2021

Dvacáté století – století velkolepých objevů, vynálezů umožňujících nové podrobnější bádání – zaznamenalo velký rozmach a uplatnění vědy. Praktické užití nachází i rozpracovaný matematický aparát. Fyzikové, chemici i biologové prohlížejí přírodu ze všech stran a vytrácí se názor z konce 19.století, že se už nic převratného nedá objevit.

Snad to byl právi rozvoj vědy, který do novověké společnosti vnesl i zvláštní krizi nejvíce patrnou v první polovině našeho století. Otázky o původu a smyslu života – objektivní pravdy o světě – patří asi mezi ty nejpodstatnější. Vznikl však pocit, že věda končí tam, kde začíná reálný svět – pravda, a tento pocit byl prvním příznakem vznikající krize. Nové poznatky převážně přírodních věd způsobily rozdvojení na dva světy. První, ve kterém žijeme, v nimž se orientujeme, aniž bychom se museli snažit chápat jeho podstatu, a druhý – svět vědy, matematicky formulovaných zákonů a idealizovaných modelů. Názory, že náš svět je nedokonalý, protože je nepřesný, byly známkou pochybnosti o racionalitě samé. Svět, ve kterém žijeme, ztrácela věda z očí a stávala se jen jakousi „služkou techniky“.

Vědci však nespali na vavřínech. Rozvíjí se kvantová mechanika, molekulární biologie, kybernetika … a výpočetní technika, která se stává stále používanějším nástrojem. Koncem šedesátých let to byly právě „moderní“ počítače, které umožnily dát i poměrně složitým matematickým modelům názornou podobu. Výpočetní rychlost počítačů neustále vzrůstala, počítače byly menší, levnější a tím i přístupnější.

Ještě před několika lety bylo velice obtížné názorně ukázat určité vlastnosti matematicky popsaného systému. Mnohdy byl člověk odkázán jen na svou představivost a fantazii, některé problémy byly z časových důvodů neřešitelné. Výpočty, které by kdysi zabraly několik měsíců, ba i let úmorné práce, provede dnes počítač téměř okamžitě a na monitoru pak spatřujeme dříve pro mnohé nepředstavitelné. V počítačem simulovaných modelech se náhle začaly projevovat jevy, které známe z běžného života.

Deterministický chaos

Dynamické systémy jsou matematické modely systému měnících se v čase. Vhodnými modely lze simulovat průběhy celé řady dějů – nejen matematických, fyzikálních či chemických, ale i biologických, ekonomických … Časový průběh systému bývá různý. Někdy se ustálí na jediné hodnotě, jindy se jich pravidelně střídá víc, ale v poslední době nejatraktivnější případ je ten, kdy se hodnoty mění zcela „náhodně“ – chaoticky. Hovoříme o systémech citlivých vůči počátečním podmínkám, kde každá i nepatrná změna úvodního nastavené (počátečních podmínek) vede po určitém časovém průběhu ke zcela odlišným hodnotám. Tento jev byl nazván paradoxně deterministický chaos.

Chaotické chování však nemusí vznikat jen ve složitých systémech, jaké známe v přírodě. Pro názornost postačí, zaměříme-li se na nejjednodušší nelineární systém – reálnou parabolu (s rovnicí x = Rx(1-x) ). Již v roce 1842 se zabýval tímto problémem nizozemský matematik Verhulst a došel k velice zajímavým výsledkům.
Hledáním iteračního řešení rovnice x = Rx(1-x) pro určité parametry R nalezl hodnoty, které rovnici nesplňují, ale řešení k nim JE „jakoby přitahováno“. Zajímavé vlastnosti této rovnice zkoumal i M. Fiegenbaum – jeho experimenty, které prováděl jen s pomocí kalkulačky, ho dovedly k zákonitostem později teoreticky potvrzeným. Matematik John von Neuman používal v roce 1942 ke generování náhodných čísel obdobný výraz: f(x) = 4x(1-x), tato funkce běžící nezávisle na ostatních programech po zavolání „náhodně vyhodila“ číslo z intervalu (0,1).

Reálná parabola

Vyzkoušejte si jednoduchou rovnici (nebo posloupnost, chcete-li) která je dána předpisem:

**f(x_n+1) = 4x_n(1-x_n)**

kde x_n+1 je nový prvek řady [x0, x1, x2, … xn], který se vypočítá z předchozího – pomocí jednoduchého předpisu:
4*x_n*(1 – x_n) (symbol * pro násobení se používá v mnoha programovacích jazycích)

Zvolíme například výchozí (nultý) člen posloupnosti roven 0,1
x₀ = 0,1

potom první člen:
x₁= 4 * x₀ * (1-x₀) = 4 * 0,1 * (1 – 0,1) = 0,36

dále pak
x₂ = 4 * x₁ * (1-x₁) = 4 * 0,36 * (1 – 0,36) = 0,9216
x₃ = 0,28901…

a dostáváme posloupnost „náhodných“ čísel z intervalu 0 – 1 / dnes (2012+) se jim již říká pseudonáhodná.

Výše popsaný nelineární systém může být například zjednodušeným modelem růstu populace na omezeném teritoriu. Stav nové populace x je dán populačním přírůstkem Rx a výraz (1-x) vyjadřuje faktor přemnožení.
Zajímá-li nás časový vývoj tohoto systému. Jde vlastně o řešení rovnice iterační metodou.

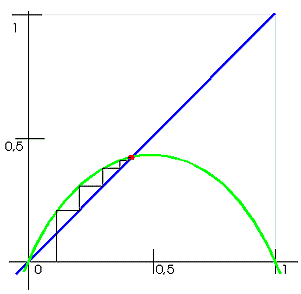
Dynamický systém reálné paraboly tvoří již výše zmíněná rovnice: x = Rx(1-x).
Její grafické znázornění je velice snadné. Hledáme průsečík modré přímky y=x a zelené paraboly y=Rx(1-x), jejíž vrchol má souřadnice (1/2, R/4).

Přepis pro její iterační řešení je dán zobrazením:
f(x) = Rx(1-x) nebo Xn+1 = f(Xn) = Rxn(1-xn),
ze kterého získáme posloupnost xo, f(xo), f(f)xo)),…

Každý nový člen posloupnosti počítáme z předchozího členu dosazením do f(x), kde je zobrazení (funkce) dané parabolou a xo je počáteční „odhad“ nebo nastavení – první hodnota.
(Schodovité průběhy na obrázcích 1-4)

Pro iteraci musíme zvolit počáteční odhad – například xo=0,1. Je-li parametr R = 1, řešení konverguje k nule. Tímto triviálním případem se nebudeme zabývat.
Populace s takto malým přírůstkem by po určitém čase vyhynula.

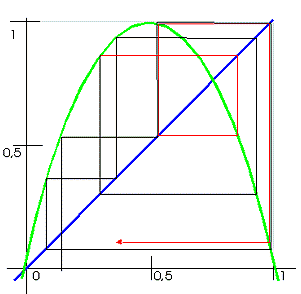
Na obrázku 1 je systém (pro R= 1.9) ve stavu, kdy po několika krocích (schodovitý průběh, spojující body (xo, O), (xo, f(xo)), (f(xo), f(xo)),… dospěje k jedinému bodu – řešení xe (červený bod na obr.1).
Jedná se o stav, pro který platí f(xe)=xe, tzv. pevný bod zobrazení.

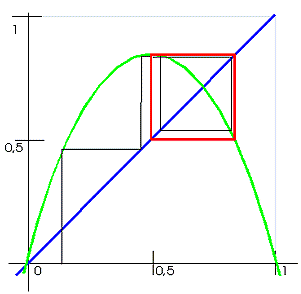
Při zvětšení parametru na R=3.3 (obr.2) se místo netriviálního řešení objeví atraktor. Tento atraktor už není řešením, ale soustava je k němu „přitahována“.
Populace s tímto parametrem bude oscilovat mezi dvěma stavy – například: první rok se mírně přemnoží a další rok se z důvodu nedostatku potravy její stav sníží.
Na obrázku je cyklus zobrazen červeným obdélníkem. Je to názorný příklad bifurkace – rozdvojení délky cyklu – nejzákladnějšího kamene cesty k chaotickému chování, což si ukážeme na obrázku č.5).

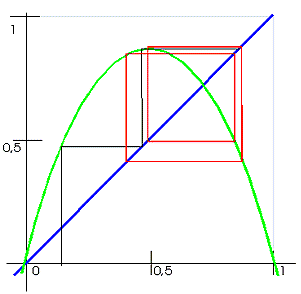
Při dalším zvětšení parametru došlo k další bifurkaci (obr.3), atraktor tentokrát tvoří červený „čtyřcykl“ (opět zobrazen červeně)

Pro parametr R=4 (obr.4) vzniká chaotický atraktor.

O populaci s touto hodnotou parametru nemůžeme ze znalosti počátečního stavu předvídat další vývoj.
Systém je v této oblasti neuvěřitelně citlivý na počáteční podmínky – odtud název systém citlivý vůči počátečním podmínkám, a jeho řešení vede mnohdy na chaotické atraktory.

Jiné zajímavé vlastnosti popsal M. Feigenbaum. Zjistil, že pro R=3,5699456 má systém nekonečný atraktor, podobný nekonečnému cyklu.
Body tvořící hranici přitažlivosti atraktoru jsou fraktální množinou (podobnou cantorovu diskontinuu). Ale to je už vyšší matematické hraní i nad možnosti chápání mnohých současných matematiků.

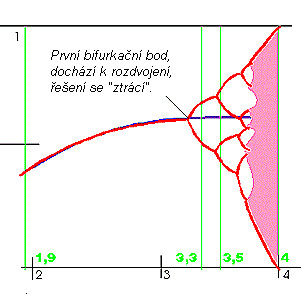
Na tomto obrázku je bifurkační diagram zobrazující závislost atraktoru na daném parametru. Pro přehlednost není prvních sto iterací bráno v úvahu, vidět je až další „ustálená“ část. Zřetelné je postupné rozdvojování, které vede k chaotickému průběhu. Ani v oblasti chaosu není dynamika systému nijak jednotvárná. Střídají se části chaosu s pravidelnými cykly – nikdy dokonce cykly liché délky.
Předchozí ukázky pro parametry 1,9 – 3,3 – 3.5 – 4 jsou zobrazeny jako „řezy“ zeleně.

Vykazuje-li poměrně jednoduchý systém tolik rozmanitých možností vývoje, jak je to potom se složitými systémy nebo dokonce s jejich soustavami?

Teoretický biolog R.M.May ocenil význam příkladu reálné paraboly:

„Už v ranném stádiu matematického vzdělání by se studenti měli seznámit s touto rovnicí. Nejen ve vědě, ale i v každodenním světě ekonomiky a politiky by bylo lepší, kdyby více lidí vědělo, že jednoduché nelineární systémy nemusejí mít nutně jednoduché chování“.

Mandelbrodtovo jablko

Přidáním dalšího rozměru můžeme pomocí počítače vstoupit do tajemné krajiny Mandelbrodtovy množiny, což je zajímavý příklad tentokrát komplexní paraboly tvaru:

f(z) = z²+c

kde f(z) je posloupnost komplexních čísel. Tato opravdu „krásná“ fraktální množina je velice populární – barevné pohledy do jejího nitra jsou velice působivé. Jednoduchými výpočty pomocí počítače zjišťujeme, jak se chová komplexní číslo (charakterizované dvojicí čísel komplexní roviny, proto se v rovině dají snadno vizualizovat).
Projíždíme jeden bod roviny po druhém a vypočtené body řadíme do skupin (odlišených barvou) podle toho, jak dlouho setrvávají v jisté oblasti. Nacházíme body ustálené, stabilní, méně stabilní nebo-li bloudivé.

Přiřadíme-li bodům stabilním určitou barvu, bodům méně stabilním barvy jiné podle míry nestability, dostáváme v rovině body s různými barvami.

Tato množina je velice zvláštní, ponoříme-li se hlouběji do jejího nitra (zvolíme konkrétní malý interval zobrazení) nacházíme ruzné „fraktální stromy“, spirály, a můžeme opět narazit na výchozí tvar „jablka“ v různých modifikacích. Odtud název Mandelbrodtovo jablko.

https://www.youtube.com/watch?v=PD2XgQOyCCk

Existují i další modifikace a různé nastavení parametrů.
Ponořte se do deterministického chasu a přemýšlejme, nad množstvím informace, které se může ukrývat v jednoduchých matematických rovnicích:

Autor: Ing. Jan Čopák – Z předmluvy a úvodu diplomové práce „Stochastické chování deterministických systémů“ – zjednodušeno pro Vědu techniku mládeže v roce 1997, pro CD MATEMATIKA v roce 2001, a pro server Cereatores v roce 2014, nyní 2020 pro server Agama point.com a následně pro workshop na Hackers kongersu v Paralelní Polis – Praha 2021.

.:.